一

前兩天，有人專程跑到我的文章《類與封裝》留言，說(shuō)數(shù)據(jù)結(jié)構(gòu)更加抽象，更加穩(wěn)定，因而OO的封裝不make sense。為了證明其觀點(diǎn)，還專門引用了Fred Brooks在《人月神話》里的敘述：

Show me your flowcharts, and conceal your tables, and I shall continue to be mystified; show me your tables and I won't usually need your flowcharts: they'll be obvious.
-- Fred Brooks, "The Mythical Man Month", chapter 9

這位朋友的觀點(diǎn)其實(shí)并不鮮見(jiàn)：我已經(jīng)見(jiàn)過(guò)太多的反OO碼農(nóng)，以此為證據(jù)，來(lái)支持其“OO無(wú)用，封裝無(wú)用，對(duì)數(shù)據(jù)結(jié)構(gòu)的直接依賴更好...”諸如此類的結(jié)論。而那位朋友更是在回復(fù)中對(duì)眾人呼吁：作為程序員，不要學(xué)什么OO，SOLID……

而每次聽(tīng)到這類宗教戰(zhàn)爭(zhēng)般的言論，我都會(huì)一邊苦笑，一邊心里嘀咕：這些人真正負(fù)責(zé)過(guò)復(fù)雜一點(diǎn)的系統(tǒng)開(kāi)發(fā)，交付和維護(hù)么？

二

事實(shí)上，強(qiáng)調(diào)數(shù)據(jù)結(jié)構(gòu)比算法更重要的觀點(diǎn)，我還可以舉出更多。

比如Linus Torvalds在一封郵件里所表達(dá)的觀點(diǎn)：

(*) I will, in fact, claim that the difference between a bad programmer
and a good one is whether he considers his code or his data structures
more important. Bad programmers worry about the code. Good programmers
worry about data structures and their relationships.

再比如，在《The Art of Unix Programming》里，也表達(dá)了類似的觀點(diǎn)：

Rule of Representation: Fold knowledge into data so program logic can be stupid and robust.

Even the simplest procedural logic is hard for humans to verify, but quite complex data structures are fairly easy to model and reason about. To see this, compare the expressiveness and explanatory power of a diagram of (say) a fifty-node pointer tree with a flowchart of a fifty-line program. Or, compare an array initializer expressing a conversion table with an equivalent switch statement. The difference in transparency and clarity is dramatic. See Rob Pike's Rule 5.

Data is more tractable than program logic. It follows that where you see a choice between complexity in data structures and complexity in code, choose the former. More: in evolving a design, you should actively seek ways to shift complexity from code to data.

The Unix community did not originate this insight, but a lot of Unix code displays its influence. The C language's facility at manipulating pointers, in particular, has encouraged the use of dynamically-modified reference structures at all levels of coding from the kernel upward. Simple pointer chases in such structures frequently do duties that implementations in other languages would instead have to embody in more elaborate procedures.

如果愿意，我還可以舉出更多。

我從未懷疑過(guò)這些觀點(diǎn)的正確性，而這也正是我的觀點(diǎn)。

三

首先，所有這些被引用的觀點(diǎn)，其實(shí)都是在強(qiáng)調(diào)：數(shù)據(jù)的清晰性。

任何一個(gè)有經(jīng)驗(yàn)，有sense的程序員，都會(huì)承認(rèn)數(shù)據(jù)結(jié)構(gòu)的重要性。一個(gè)良好定義的數(shù)據(jù)結(jié)構(gòu)以及它們之間的關(guān)系，往往比算法更清晰。

這是因?yàn)椋粋€(gè)良好的數(shù)據(jù)結(jié)構(gòu)定義所要表達(dá)的概念，以及概念之間的關(guān)系，是一種高度結(jié)構(gòu)化的信息。而我們?nèi)祟惖拇竽X，最善于理解的就是這類信息。相對(duì)于不那么結(jié)構(gòu)化的，代表算法的流程圖，實(shí)體關(guān)系圖所需的智商指數(shù)要低的多。

而反過(guò)來(lái)，有了這些高度結(jié)構(gòu)化的數(shù)據(jù)結(jié)構(gòu)之后，我們就更容易推理和理解圍繞這些數(shù)據(jù)結(jié)構(gòu)的算法。

這也正是我們?cè)诜治鲆粋€(gè)業(yè)務(wù)領(lǐng)域，建立其領(lǐng)域模型時(shí)，靜態(tài)視圖：包含類（概念實(shí)體）以及類與類之間的關(guān)系，對(duì)于理解一個(gè)領(lǐng)域至關(guān)重要的原因。

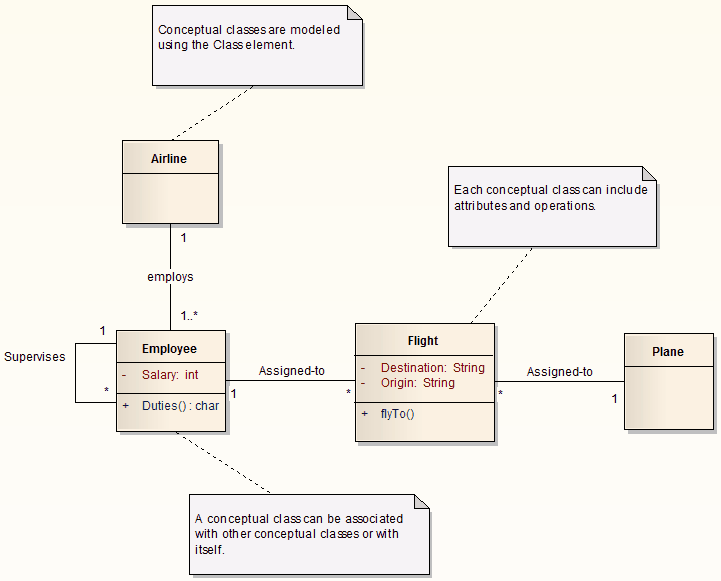領(lǐng)域?qū)ο竽Ｐ?/div>

當(dāng)然，這一切，都是建立在一個(gè)良好的領(lǐng)域分析基礎(chǔ)上的。作為咨詢師，我見(jiàn)過(guò)太多團(tuán)隊(duì)，根本不重視數(shù)據(jù)結(jié)構(gòu)的定義，完全不考慮數(shù)據(jù)結(jié)構(gòu)所代表的概念，也不考慮數(shù)據(jù)的內(nèi)聚性，只見(jiàn)到系統(tǒng)堆滿了隨機(jī)而凌亂的數(shù)據(jù)結(jié)構(gòu)，從而讓系統(tǒng)極難理解。

這也正是為何Linus強(qiáng)調(diào)：糟糕的程序員更關(guān)注代碼（算法）；而優(yōu)秀的程序員更關(guān)注數(shù)據(jù)結(jié)構(gòu)和它們之間的關(guān)系。

數(shù)據(jù)結(jié)構(gòu)定義的重要性，怎么強(qiáng)調(diào)都不為過(guò)。

四

數(shù)據(jù)結(jié)構(gòu)，相對(duì)于算法，不僅更清晰，在大多數(shù)情況下甚至?xí)?strong>穩(wěn)定。

首先，我們先看一個(gè)簡(jiǎn)單的例子。如下代碼定義了一個(gè)數(shù)據(jù)結(jié)構(gòu)Rectangle：

struct Rectangle
{
    unsigned int height;
    unsigned int width;
};

不難發(fā)現(xiàn)，這個(gè)用來(lái)表現(xiàn)矩形的數(shù)據(jù)結(jié)構(gòu)，是非常清晰的。

而圍繞它的算法，相對(duì)于它的數(shù)據(jù)，卻更加不穩(wěn)定。比如，現(xiàn)在某個(gè)需求需要求它的周長(zhǎng)，因而，我們需要提供一個(gè)算法：

unsigned int calcPerimeter(Rectangle* rect)
{
    return (rect->height + rect->width) * 2;
}

當(dāng)然，也可以將算法實(shí)現(xiàn)為：

unsigned int calcPerimeter(Rectangle* rect)
{
    return rect->height * 2 + rect->width * 2;
}

或者：

unsigned int calcPerimeter(Rectangle* rect)
{
    return rect->height + rect->height + rect->width + rect->width;
}

不難看出，對(duì)于同一個(gè)需求，我們可以基于同一個(gè)數(shù)據(jù)結(jié)構(gòu)，給出不同的算法實(shí)現(xiàn)。因而，在這個(gè)例子中，數(shù)據(jù)結(jié)構(gòu)比算法更清晰，也更穩(wěn)定。

但這是否就意味著，封裝對(duì)于Rectangle就沒(méi)有意義？

五

對(duì)于一個(gè)軟件系統(tǒng)，單純的數(shù)據(jù)結(jié)構(gòu)是沒(méi)有太多意義的（除非它只是一個(gè)數(shù)據(jù)展現(xiàn)系統(tǒng)）。數(shù)據(jù)結(jié)構(gòu)和算法，都是為客戶的根本需要而服務(wù)。沒(méi)有客戶的需要，則數(shù)據(jù)結(jié)構(gòu)和算法，無(wú)論誰(shuí)更清晰，更穩(wěn)定，都沒(méi)有任何意義。一個(gè)數(shù)據(jù)結(jié)構(gòu)該怎么定義，一個(gè)算法該如何設(shè)計(jì)，這一切都是從客戶的需要出發(fā)，結(jié)合各種約束，程序員作出的選擇而已。

比如，同樣都是矩形，如果現(xiàn)在我們正在做的是一個(gè)畫圖系統(tǒng)，則其數(shù)據(jù)并不必然使用width和height來(lái)表示，這時(shí)候，使用坐標(biāo)位置，或向量來(lái)表示矩形，會(huì)是更合理的選擇。

因而，盡管在不同領(lǐng)域里，有可能都能挖掘出相同的領(lǐng)域概念，以及相同的領(lǐng)域概念間關(guān)系。但其具體數(shù)據(jù)（屬性），卻會(huì)伴隨著不同領(lǐng)域的需求不同而不同。

另外，即便在同一個(gè)領(lǐng)域，對(duì)于同樣的業(yè)務(wù)需求，當(dāng)定義數(shù)據(jù)結(jié)構(gòu)時(shí)，往往也會(huì)由于性能，空間，便利性等非功能性需求和設(shè)計(jì)約束，而作出不同的決定。比如，同樣都是1..N的關(guān)系，我究竟該選擇Array還是List？如果選擇List，改選單向，還是雙向？對(duì)于每個(gè)有經(jīng)驗(yàn)的C,C++開(kāi)發(fā)者，這都是做一個(gè)真實(shí)系統(tǒng)時(shí)經(jīng)常需要考慮的問(wèn)題。

我們已經(jīng)知道，Linus極其重視數(shù)據(jù)結(jié)構(gòu)的定義，如果我們?nèi)タ?code>Linux Kernel的設(shè)計(jì)，就能知道，其數(shù)據(jù)結(jié)構(gòu)的選擇，和數(shù)據(jù)間的關(guān)聯(lián)選擇，會(huì)多大程度上受到非功能因素的影響。否則，那些數(shù)據(jù)結(jié)構(gòu)的定義會(huì)更加清晰，穩(wěn)定和簡(jiǎn)單。

但你無(wú)論如何選擇，最終都是為了滿足客戶的業(yè)務(wù)需要。

六

回到我們的Rectangle。從需求出發(fā)，我們的系統(tǒng)存在Rectangle這個(gè)概念，那么客戶需要這個(gè)概念的真正原因是什么？是Rectangle的數(shù)據(jù)結(jié)構(gòu)，還是calcPerimeter內(nèi)部的算法？

答案是：都不是。

客戶真正需要，也真正依賴的是API: unsigned int calcPerimeter(Rectangle* rect)，而不是Rectangle的數(shù)據(jù)結(jié)構(gòu)，更不是calcPerimeter的算法實(shí)現(xiàn)。

雖然數(shù)據(jù)結(jié)構(gòu)比算法實(shí)現(xiàn)更穩(wěn)定，但它再穩(wěn)定，相對(duì)于API，也依然只是一種實(shí)現(xiàn)細(xì)節(jié)。

而讓客戶向著更穩(wěn)定的方向依賴（參見(jiàn)《變化驅(qū)動(dòng)：正交設(shè)計(jì)》），從而依賴API，而不是直接依賴數(shù)據(jù)結(jié)構(gòu)，這就是封裝的核心價(jià)值。

封裝

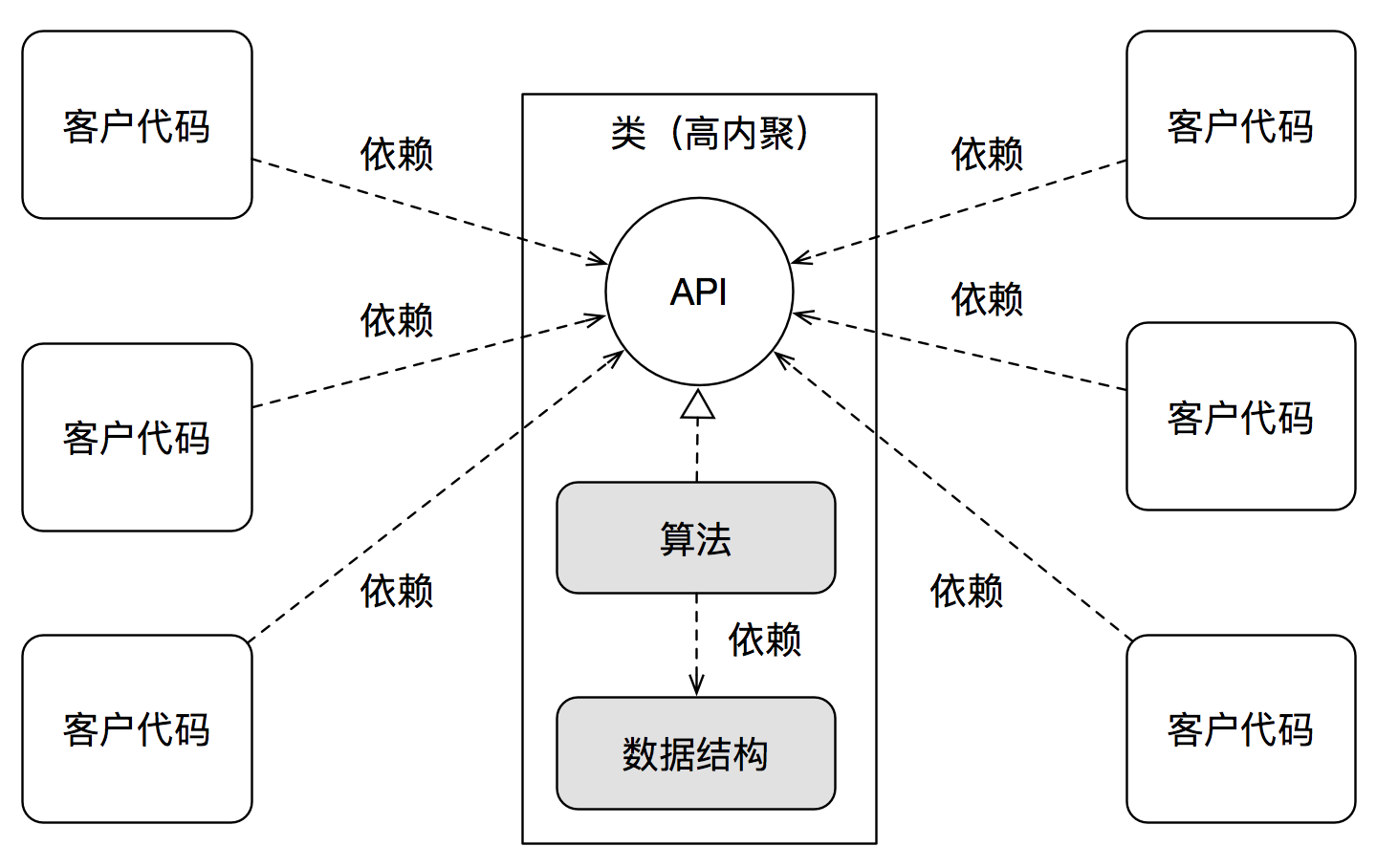
而如果不進(jìn)行封裝，客戶擁有訪問(wèn)數(shù)據(jù)，并定義算法的自由，就會(huì)讓客戶同時(shí)依賴數(shù)據(jù)結(jié)構(gòu)和算法。無(wú)論你認(rèn)為數(shù)據(jù)結(jié)構(gòu)更不穩(wěn)定，還是算法更不穩(wěn)定，總之都會(huì)讓用戶直接依賴在不穩(wěn)定的事物上。同時(shí)，在大產(chǎn)品下，極易造成重復(fù)，這會(huì)進(jìn)一步導(dǎo)致更嚴(yán)重的耦合（見(jiàn)《類與封裝》）。

當(dāng)數(shù)據(jù)結(jié)構(gòu)和算法還在爭(zhēng)論誰(shuí)更抽象，更穩(wěn)定時(shí)，API笑了。

七

而最最重要的部分，在Grady Booch著名的《面向?qū)ο蠓治雠c設(shè)計(jì)》中，對(duì)OOP定義的第一個(gè)要點(diǎn)則是：

利用對(duì)象作為面向?qū)ο缶幊痰幕具壿嫎?gòu)建塊，而不是利用算法。

這與把Procedure看做Building Block的面向過(guò)程范式，把Function看做Building Block的函數(shù)式范式相比，如果我們認(rèn)為數(shù)據(jù)結(jié)構(gòu)比算法更穩(wěn)定是一個(gè)事實(shí)，那么毫無(wú)疑問(wèn)，面向?qū)ο?/strong>才是更加尊重這個(gè)事實(shí)的范式。