注:本文原名《OO NOT SUCKS, YOU DO》。
緣起
Erlang之父Joe Armstrong曾經寫過一篇《Why OO Sucks》,被很多反OO的程序員——尤其是erlang社區的程序員——當作了大旗。
文中指出了OO的四大問題:
- 數據結構和函數不應被綁在一起(
Data structure and functions should not be bound together); - 所有事物都不得不是對象(
Everything has to be an object); - 在面向對象語言里,數據類型定義散播在各處(
In an OOPL data type definitions are spread out all over the place); - 對象有私有狀態(
Objects have private state)。
做為一個已經關注OO與FP都將近10年的老鳥(包括erlang),我對此的看法是:這四大問題里,除了第二條尚可商榷之外,其它幾條都只是證明了Joe并不明白什么是面向對象,甚至都不明白什么叫高內聚,低耦合。
一個例子
Joe在其著作《Programming Erlang》里,給出一個下面的例子:
area({rectangle, Width, Ht}) -> Width * Ht;
area({circle, R}) -> 3.14159 * R * R;
area({square, X}) -> X * X.
這個例子充分反映了Joe對于程序設計的看法:
- 數據結構和算法是分離的;
- 沒有私有狀態,所有的數據結構信息都是公開的;
- 對于不同類型數據的類似操作應該被放在一起。
接著,為了證明Erlang的簡練,Joe給出了一個C語言的實現:
enum ShapeType { Rectangle, Circle, Square };
struct Shape {
enum ShapeType kind;
union {
struct { int width, height; } rectangleData;
struct { int radius; } circleData;
struct { int side; } squareData
} shapeData;
};
double area(struct Shape* s) {
if( s->kind == Rectangle ) {
int width, ht; width = s->shapeData.rectangleData.width;
ht = s->shapeData.rectangleData.ht;
return width * ht;
} else if ( s->kind == Circle ) {
// ...
} else if ( s->kind == Square ) {
// ...
}
}
Joe認為這是一個與Erlang版本思想一致的C實現。都是使用模式匹配。差別只在于,Erlang的版本要比C版本要簡練的多。
然后Joe又給出了一個Java的版本:
abstract class Shape {
abstract double area();
}
class Circle extends Shape {
final double radius;
Circle(double radius) { this.radius = radius; }
double area() { return Math.PI * radius*radius; }
}
class Rectangle extends Shape {
final double ht;
final double width;
Rectangle(double width, double height) {
this.ht = height; this.width = width;
}
double area() { return width * ht; }
}
class Square extends Shape {
final double side;
Square(double side) {
this.side = side;
}
double area() { return side * side; }
}
通過這個例子,Joe除了想說明Java版本比Erlang版本更為繁瑣之外,更是為了證明之前批評OO的理由,在面向對象語言里,數據類型定義散播在各處:Java版本的三個類定義被放在三個不同的文件里。
Joe對OO的所有批評都是集中在現象級(包括他對OOPL的批評,錯誤的把某種OO語言的現象當做OOPL本身),卻沒有深入到軟件設計的挑戰,目標和解決方案一級來探討。這也是他寫出那篇充滿謬誤的文章的最根本原因。
回到這三個實現,事實上是三種不同的設計思路(不僅僅是語言造成的實現差異)。這一切,還需要從本源說起。
選擇問題
軟件開發中,存在著大量的選擇問題。所以,結構化的語言都提供了諸如if-else,switch-case的語法結構;C/C++的預處理則提供了#if,#ifdef,#else等控制結構;而其它語言,比如 Erlang,Haskell等則提供了模式匹配作為選擇方式;而 Makefile也提供了if-else結構,讓程序的構建者可以選擇不同的構建方式。
而選擇問題恰恰是程序的復雜度和管理難度所在。很多時候,如果程序過于依賴這些if-else式的控制結構,會讓一段代碼過于依賴具體的細節,從而造成這些代碼需要不斷修改,無法做到開放封閉,也有害于代碼的重用。
隔離細節(也意味著隔離變化)的方法當然是抽象。程序員們試圖通過抽象的手段,將 if-else, switch-case所表達的不同事物,統一為某個一致的概念。然后,當前代碼就可以對那些不同事物進行一致的操作,從而將if-else式的選擇過程踢出當前代碼。
但這并不意味著選擇的過程消失了,它們只是被從當前代碼中被分離出去(分離不同變化方向)。而這種分離就保證了當前代碼不再受選擇過程的干擾。
這種處理問題的思路,被稱為多態。其定義為: 同一外表之下的多種形態。結合之前的描述,可以總結出多態思想的四個關鍵元素:
- 客戶代碼(用戶)
- 同一外表(抽象)
- 不同形態(細節)
- 形態選擇(映射)
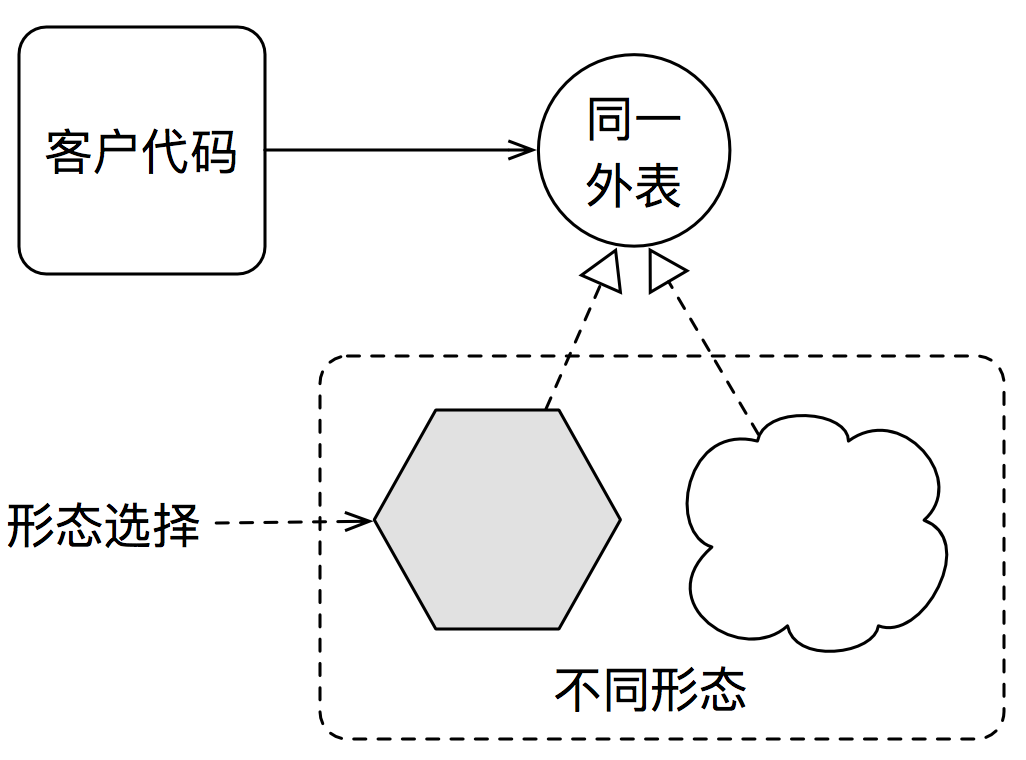
從之前的描述及這幅圖也可以清晰的看出:
- 形態的變化,是一個選擇問題,因而與其它選擇形式,比如
if-else,switch-case,模式匹配等,可以等價轉換; - 多態通過同一外表,封裝了形態的變化;讓客戶代碼不再受形態變化的影響,從而讓系統具備更好的正交性。(多種不同形態間也是正交的)
- 形態選擇的過程,其實是一個組合的過程:把客戶代碼與某種具體形態進行組合。這是組合式設計的源泉之一。
多態與組合式設計
我一直認為,FP語言給程序員提供的最強大武器在于:極其便利的計算組合手段。比如map函數(下面例子給出的是一個haskell版本的類型注解)。
map :: (a -> b) -> [a] -> [b]
這個函數,和任何一個類型為a->b的函數進行組合,就能把一個類型為[a]的列表轉化為一個類型為[b]的列表。
C程序員則會使用callback function的方式達到類似的效果。
而基于單個函數的組合,正是一種最為樸素的運行時多態實現。
另外,Haskell的這個實現還包括了另外一種多態:參數化多態。其中a,b都是泛化的類型變量,在具體的調用時,編譯器會根據實際傳入的參數類型對a,b進行實例化。
而Erlang由于是弱類型,所以并不存在參數化多態的問題。
C++程序員,可以將其看作范型編程中的模版。事實上,模版也是一種參數化多態。
運行時多態解決的是算法變化問題;而參數化多態解決的是類型變化問題。
FP以參數化多態,以及樸素的運行時多態為基礎,構成了FP自底向上的組合設計方法:通過將一個個可以適應類型變化的小函數逐級組合,最后得到更為強大的計算功能。
OO ROCKS!!!
Erlang作為一門FP語言,想必Joe一定是認可基于運行時多態的設計思想的。
而運行時多態,作為OO關鍵特征之一,則提供了更為強大的運行時多態的支持。這里談到的強大,指的是更為便捷的隔離變化的手段。
-
OO以class為單位,可以定義一個接口集。 - 如果數據是一種實現細節,
OO可以將數據進行信息隱藏。
對于第一點:如果這組接口集正是一個概念應該提供的高內聚完整集合,我們就應該有一種直觀便利的手段來表達。
比如,Transaction DSL的公共抽象Action,其定義如下:
struct Action
{
virtual Status exec(TransactionInfo&) = 0;
virtual Status handleEvent(TransactionInfo&, const Event&) = 0;
virtual Status stop(TransactionInfo&) = 0;
virtual void kill(TransactionInfo&) = 0;
virtual ~Action() {}
};
我們知道,所謂單一職責,不僅包含前半部分:DO ONE THING,還包含后半部分DO IT WELL。如果一個概念,必須要包含多個接口才完整,那么我們沒有任何理由非要將其分離為一個個孤零零的函數;而是恰恰相反,語言需要提供一種直觀便利的手段,讓我們可以完整的定義。
而第二點,Joe認為對象有私有狀態是OO Sucks的重要原因之一。但是對實現細節進行信息隱藏,是構成了OO對提升系統正交性,促進系統局部化影響的重要手段。如下圖所示:
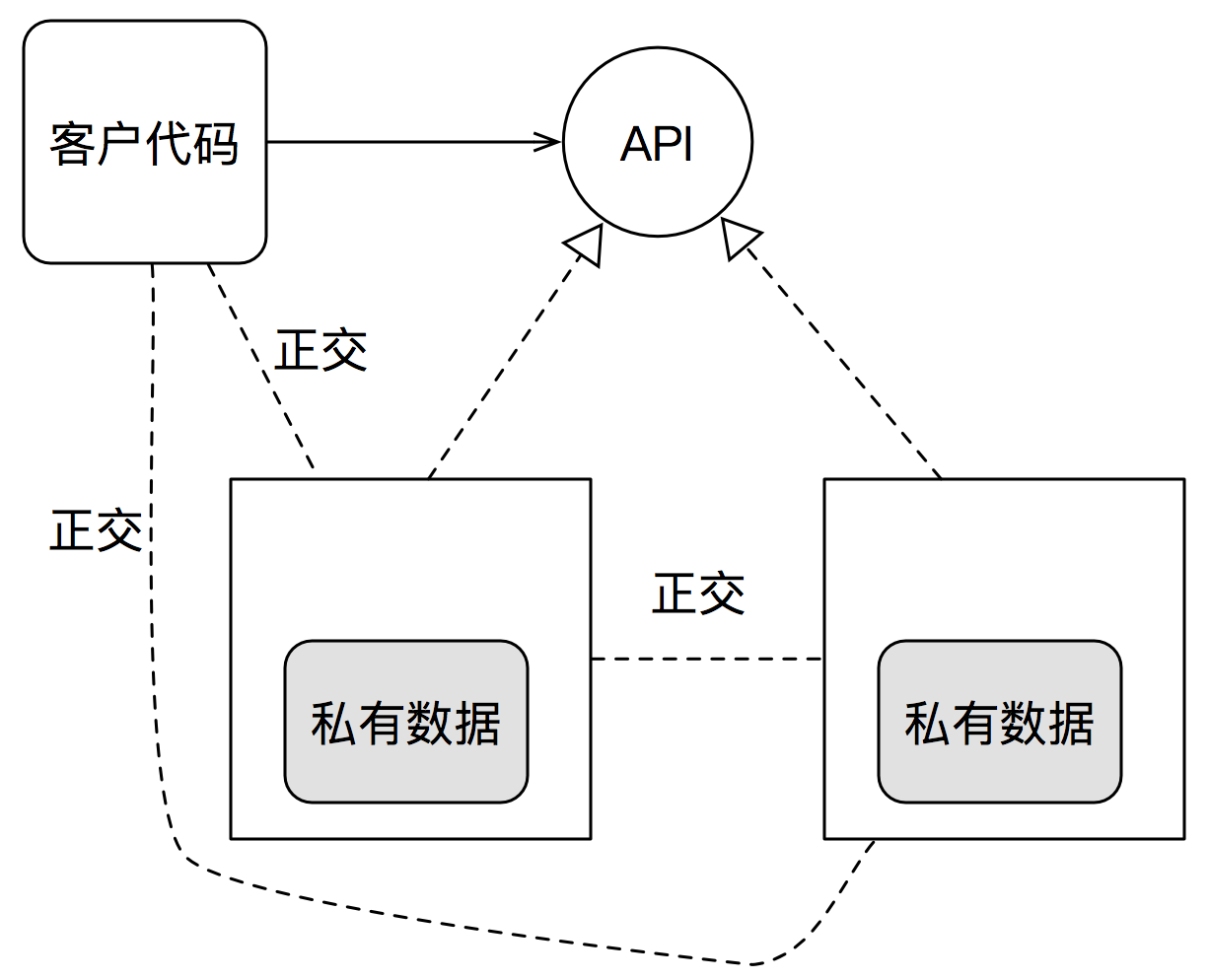
對于這一點,Joe堅持程序應該與數據分離,可是按照高內聚原則:關聯緊密的事物應該被放在一起。如果數據確實是某種算法的特定細節時,這種強制分離只會降低內聚度,提高耦合度。如下圖所示:
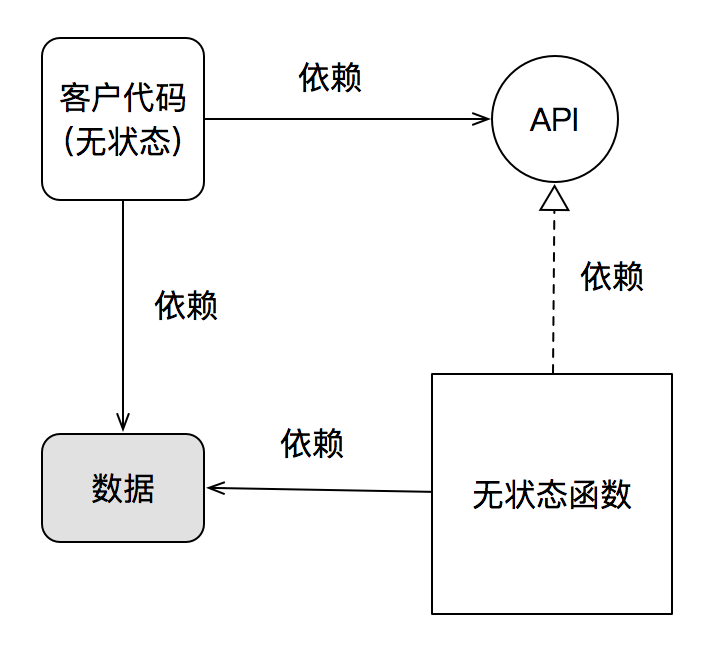
從這兩幅圖,可以清晰的看出,當數據是一種不穩定的實現細節時,對象有私有狀態與數據與程序分離對于系統耦合度的不同影響。
所以,如果站在Joe對于OO批評的論據出發,不僅不會得到OO Sucks的結論,而是恰恰相反:OO ROCKS!!
AD-HOC多態 vs. SUBTYPE多態
現在,讓我們回到Joe在其著作中給出的例子:
area({rectangle, Width, Ht}) -> Width * Ht;
area({circle, R}) -> 3.14159 * R * R;
area({square, X}) -> X * X.
這是個模式匹配的版本。模式匹配也是一種多態:ad-hoc多態。
而之前例子中Java的版本,則是我們熟知的subtype多態。
按照Joe的觀點,Erlang的版本,優于Java的版本。但這是否就意味著ad-hoc多態優于sub-type多態呢?
如果這個系統的需求復雜度就是這個樣子,不再變化,那么毫無疑問:erlang的版本明顯更簡潔。
可現實是,對于很多長生命周期的大型項目,需求變化是家常便飯。如果現在增加一個需求:對于所有Shape,增加一個求周長的需求。
這難不倒Erlang程序員,很快,他們就在同一個文件里(這正是Joe所倡導的),寫下了如下代碼:
perimeter({rectangle, Width, Ht}) -> 2 * (Width + Ht);
perimeter({circle, R}) -> 2 * 3.14159 * R;
perimeter({square, X}) -> 4 * X.
而使用Java,則修改如下:
interface Shape {
// untouched code
double perimeter();
}
class Circle extends Shape {
// untouched code
double perimeter() { return Math.PI * 2 * radius; }
}
class Rectangle extends Shape {
// untouched code
double perimeter() { return (width + ht) * 2; }
}
class Square extends Shape {
// untouched code
double perimeter() { return 4 * side; }
}
我們可以看出,從工作量的角度,兩者差不多。區別在于,Erlang版本,只需要在一個地方羅列三種實現;而Java版本則需要到四個文件進行同步修改。好在,如果某個子類在修改時被遺漏,編譯器會報錯。這會強迫程序員對所有子類都進行修改,不會遺忘。這一局,Erlang繼續保持優勢。
現在,我們考慮另外一個變化方向:如果現在增加一個新的Shape,比如Triangle。
則Erlang需要做的修改是:
area({rectangle, Width, Ht}) -> Width * Ht;
area({circle, R}) -> 3.14159 * R * R;
area({square, X}) -> X * X;
area({triangle, Data}) -> ... .
perimeter({rectangle, Width, Ht}) -> 2 * (Width + Ht);
perimeter({circle, R}) -> 2 * 3.14159 * R;
perimeter({square, X}) -> 4 * X;
perimeter({triangle, Data}) -> ... .
需要修改area和perimeter兩個函數的實現。
而Java則無需改動任何原有代碼,只需要增加一個新的類:
class Triangle extends Shape {
// Data
double area() { ... }
double perimeter() { ... }
}
在這個變化方向上,Java版本對于系統的影響程度,要小于Erlang版本。
由此,我們可以知道,從兩者受變化影響程度角度看:
-
如果擴展一個操作,
ad-hoc多態優于subtype多態; -
如果擴展一個類型,
subtype多態優于ad-hoc多態。
到目前為止,兩者平分秋色。
我們再看看其它的變化:如果某個Shape的數據發生了變化,比如,Triange的數據從Data變化為Data1。則Erlang的代碼需要到兩個地方修改:
area({rectangle, Width, Ht}) -> Width * Ht;
area({circle, R}) -> 3.14159 * R * R;
area({square, X}) -> X * X;
area({triangle, Data1}) -> ... .
perimeter({rectangle, Width, Ht}) -> 2 * (Width + Ht);
perimeter({circle, R}) -> 2 * 3.14159 * R;
perimeter({square, X}) -> 4 * X;
perimeter({triangle, Data1}) -> ... .
而Java版本則只需要修改一個類:
class Triangle extends Shape {
// Data1
double area() { ... }
double perimeter() { ... }
}
subtype多態再勝一局。
更何況,subtype版本的四個Shape都各自隱藏了自己的數據格式。客戶代碼不可能對這些數據產生任何依賴。客戶只依賴Shape所提供的API。
而Erlang版本的設計,所有數據對于客戶均是公開的,客戶可以自由的訪問它們。而一旦數據格式發生了變化,BANG!!!,所有相關的代碼都需要修改。
因而,無論站在縮小依賴范圍,還是向著穩定方向依賴原則來看,subtype多態都完勝ad-hoc多態。
ADT 與 Existential Quantification
對于上面這個例子,由于erlang是弱類型,尚可以那么實現。如果使用強類型語言比如haskell,如果要使用ad-hoc多態,則必須首先讓它們類型一致化。其中一種手段是代數數據類型(ADT),比如:
data Shape = Circle Float
| Rectangle Float Float
| Square Float
area :: Shape -> Float
area (Circle r) = PI * r * r
area (Rectangle w h) = w * h
area (Square s) = s * s
perimeter :: Shape -> Float
perimeter (Circle r) = PI * r * 2
perimeter (Rectangle w h) = (w + h) * 2
perimeter (Square s) = s * 4
這樣的實現,是典型的在一處窮舉所有Shape的設計方式。每次增加,修改,刪除一個Shape,都需要來修改這里所有的代碼。
這很明顯不符合開放封閉原則。但如果這樣的情況是可窮舉且穩定的,那么這樣的設計倒也無可厚非。
但假如我們現在設計了一個框架,需要由框架的用戶自己定義和擴展具體的Shape,然后注冊給我們的框架。這時就需要一個與具體Shape無關的公共抽象。此時,ad-hoc多態不再能解決我們的問題。而subtype多態正是解決這類問題的靈丹妙藥。
在這種情況下,Joe所批評的數據類型定義散播在各處,不僅不是一個問題,而恰恰是一個最為正交的合理選擇。(當然,如果不需要將類型定義在多處時,只有Java這類的具體OO語言才有這樣的約束,而其它支持OO的語言,比如C++,完全可以將多個類型定義在一個文件里。)
而在缺乏subtype多態的強類型的系統下,這類問題很難簡單的解決。因而GHC引入了一個擴展:Existential Quantification,用來模擬subtype多態,才終于別扭的部分解決了這類問題。
關于Existential Quantification,由于篇幅問題,不再具體展開。感興趣的可查閱相關資料。
枚舉 vs. subtype多態
Joe的例子,還給出了一個C語言的使用Union和枚舉的實現,這是一種典型的模擬ADT的實現方式(Union是ADT Sum Type在C語言中的具體實現)。因而其帶來的問題也和ADT一樣。
而我們也可以從中清晰的看出:基于枚舉的實現,與基于subtype多態的實現方式之間存在著轉換關系。
正像模式匹配一樣,如果一套枚舉對應的switch-case在系統中多處存在,那就意味著,每次增加,刪除一個新的枚舉常量,都需要多處修改代碼;另外,如果某個枚舉值對應的數據結構發生了變化,也需要到多處修改代碼。
而為了做到局部化影響,則最好將枚舉修改為subtype多態的方式來解決問題。從而讓系統對于這類變化可以做到開放封閉。
結論
多態是用來應對變化,提高可重用性的重要手段。而不同多態,各自有各自的適用場景及問題。而如何取舍,則還是要用《簡單設計原則》來作為標尺。
erlang確實有其非常出色的設計:比如其虛擬機提供的輕量級進程,以及Actor Model對于高并發,分布式,高可靠的支持,可復用庫OTP對于快速構建通信類應用的支持等等都很不錯。但所有這些都并不能構成OO Sucks的理由。
事實上,完全可以存在一個系統,同樣提供相同的機制,唯獨編程語言被設定為OO語言,或者更強大的混合范式語言,這并不會削弱Erlang平臺+OTP所提供的價值,反而可能會有利于構建更加高效的,易于應對變化的系統。
而被某種具體范式的某個具體語言的某些具體特性在某些具體場景下漂亮應用所吸引,在不明覺歷、或者并未明白設計的根本出發點的情況下,狂熱的推崇一種范式,并轉而攻擊另外一種自己并不真正了解的范式,并不是一種可取的態度。(難道這個問題真的是非此即彼,非黑即白么?)
比如,C++對于ad-hoc多態,subtype多態,參數化多態,duck typing多態,預處理時多態,編譯時多態,鏈接時多態,等等各種隔離變化、有助于提高系統正交性的手段全部支持,卻總有那么一群完全沒搞懂C++的人卻在不明就里,人云亦云的批評它。
語言的復雜本身并不是壞事情,因為這個世界的問題就是那么復雜多樣,你必須擁有足夠多的手段才能高效應對。只要這些復雜度都是在幫助程序員正確高效的解決問題,那么再復雜都是好事情。只有那些沒有價值,只帶來麻煩的偶發復雜度才是問題。而讓一群沒有編程素養的人使用一門強大的工具,以至于誤用濫用,也是一個問題(問題在于,為何我們要讓沒有編程素養的程序員單獨工作?難道讓沒有設計素養的程序員使用簡單語言就會做出好設計,寫出好代碼?)。而作為追求高效開發的程序員,使用一門極其簡單,卻對很多問題缺乏高效手段的乏味工具,這才是最浪費生命,也會縮短職業生命的糟糕選擇。
因此,作為解決實際問題的程序員,首先應該深刻去理解設計本身的挑戰與目的。然后盡可能豐富自己的工具箱,讓自己持有多種武器,以便與在解決具體問題時,可以找到更為合適的手段。而不是手里持有一把錘子,則到處都是釘子。
寫在最后
在今天寫完這篇文章之時,為了添加相關的鏈接引用,無意中發現了這個消息,Joe Armstrong承認他之前那篇Why OO Sucks的文章是不成熟的,轉而宣稱Erlang才是唯一的OO語言:
Erlang has got all these things. It's got isolation, it's got polymorphism and it's got pure messaging. From that point of view, we might say it's the only object oriented language and perhaps I was a bit premature in saying that object oriented languages are about. You can try it and see it for yourself.
——Ralph Johnson, Joe Armstrong on the State of OOP
我說Joe叔,咱能別這么從一個極端走向另外一個極端好么?你讓之前跟著你喊OO sucks的人情何以堪啊…… :D