原文鏈接：A step-by-step guide to building a simple chess AI

我們先來了解一下，在我們創建一個簡單的國際象棋 AI 過程中所會接觸到的一些基本概念：

• 棋子的移動
• 繪制棋盤
• Minimax（極小化極大算法）
• Alpha-beta 剪枝

我們將一步一步將這些加入最終的算法中，并分別展示它們對算法所產生的影響。

你可以在 Github 上查看最終版本。

譯者試了下最終版本，一不小心就被吊打了...??

第一步：棋子的移動和繪制棋盤

這里我們使用 chess.js 和 chessboard.js 分別來控制棋子的移動和繪制棋盤。chess.js 庫實現了所有棋子的移動規則，基于此我們可以根據棋局狀態得到棋子所有可能的移動。

根據輸入的棋盤狀態生成所有可能的棋子移動

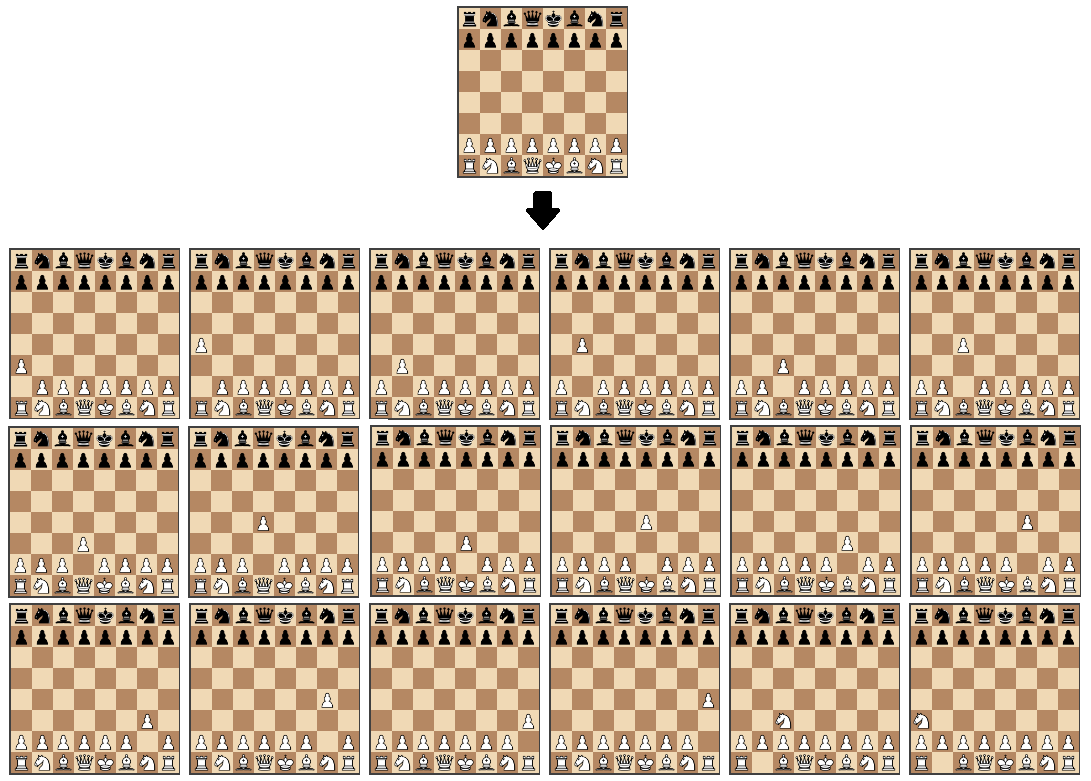
有了以上兩個類庫，我們就能將精力放在最有趣的事上——創建一個能夠找到最佳移動的 AI。

接下來就開始創建這樣一個 AI，我們先創建一個方法，它會在所有合法的移動中隨機選取一個。

var calculateBestMove =function(game) {
    //generate all the moves for a given position
    var newGameMoves = game.ugly_moves();
    return newGameMoves[Math.floor(Math.random() * newGameMoves.length)];
};

盡管，這個 AI 像一個剛懂規則的新手，但是，我們已經可以和它下棋了，這是一個好的開始。

隨機移動，[點擊試玩](https://jsfiddle.net/lhartikk/m14epfwb/4)

第二步：棋盤狀態評估

現在，我們試著計算在棋局某一狀態下哪邊更具優勢，最簡單的方法就是根據下表來統計棋局剩余棋子權重。

棋子對應權重表

根據這個方法，我們就能讓我們的 AI 選擇在棋局某一狀態下使棋局權重最高的移動了。

var calculateBestMove = function (game) {

    var newGameMoves = game.ugly_moves();
    var bestMove = null;
    //use any negative large number
    var bestValue = -9999;

    for (var i = 0; i < newGameMoves.length; i++) {
        var newGameMove = newGameMoves[i];
        game.ugly_move(newGameMove);

        //take the negative as AI plays as black
        var boardValue = -evaluateBoard(game.board())
        game.undo();
        if (boardValue > bestValue) {
            bestValue = boardValue;
            bestMove = newGameMove
        }
    }

    return bestMove;

};

加入了計算權重后，我們的 AI 就會盡可能地去吃對方的棋子。

盡可能地吃子，[點擊試玩](https://jsfiddle.net/lhartikk/m5q6fgtb/1/)

第三步：使用極小化極大算法來探索樹

下一步，我們使用 極小化極大算法(Minimax) 來使我們的 AI 能從探索樹中選出最優移動。

首先，我們先根據給定深度遞歸構建棋子所有可能移動的樹，并用上一節的方法來計算所有子節點的權重

然后，依據不同的行棋顏色，父節點取子節點的最大或最小值，若白子則取子節點的最大值返回給父節點，反之返回最小值。

深度為 2 的情況下，極小化極大算法圖解

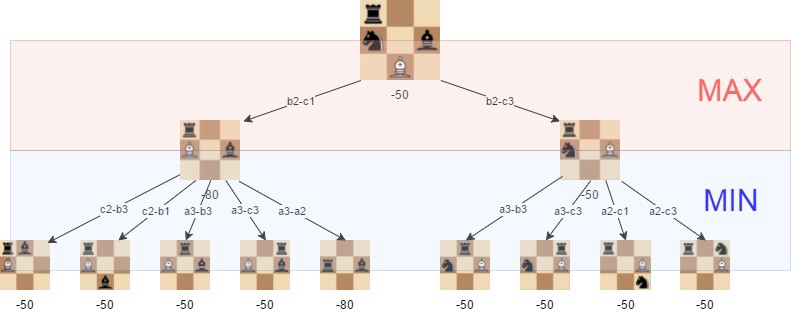
var minimax = function (depth, game, isMaximisingPlayer) {
    if (depth === 0) {
        return -evaluateBoard(game.board());
    }
    var newGameMoves = game.ugly_moves();
    if (isMaximisingPlayer) {
        var bestMove = -9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.max(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    } else {
        var bestMove = 9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.min(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    }
};

加入了極小化極大算法之后，我們的 AI 已經不再是任人宰割了。

加入了極小化極大算法，[點擊試玩](https://jsfiddle.net/lhartikk/m5q6fgtb/1/)

極小化極大算法很大程度上取決于我們能夠探索深度，下一步我們就來優化它。

第四步：Alpha-beta 剪枝

Alpha-beta 剪枝 是對極小化極大算法的一種優化，用于減少搜索樹中需要探索的節點數。這樣在同樣的資源條件下，就增加了探索樹的搜索深度。

當探索路徑的結果比之前探索的更糟時，Alpha-beta 剪枝就不再搜索該子樹。它并不影響極小化極大算法的計算結果，而是加快極小化極大算法運算速度。無論何種情況，Alpha-beta 剪枝總是能優化計算效率，即使，我們最初探索的就是最優解。

alpha-beta 剪枝用于極小化極大算法

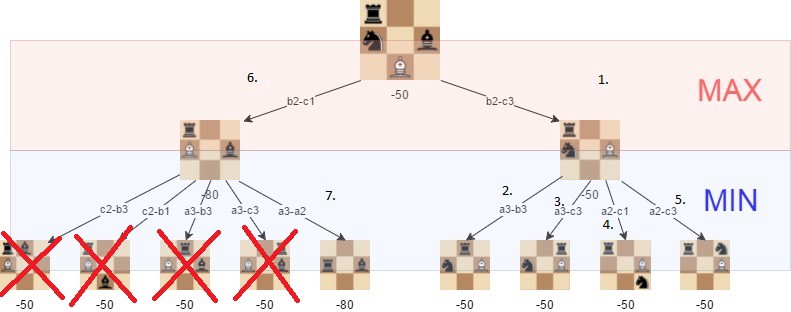
如下圖所示，通過 alpha-beta 剪枝，我們能顯著減少極小化極大算法的計算次數。

深度為 4 時，使用或不使用 alpha-beta 剪枝時的計算次數

var minimax = function (depth, game, alpha, beta, isMaximisingPlayer) {
    positionCount++;
    if (depth === 0) {
        return -evaluateBoard(game.board());
    }

    var newGameMoves = game.ugly_moves();

    if (isMaximisingPlayer) {
        var bestMove = -9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.max(bestMove, minimax(depth - 1, game, alpha, beta, !isMaximisingPlayer));
            game.undo();
            alpha = Math.max(alpha, bestMove);
            if (beta <= alpha) {
                return bestMove;
            }
        }
        return bestMove;
    } else {
        var bestMove = 9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.min(bestMove, minimax(depth - 1, game, alpha, beta, !isMaximisingPlayer));
            game.undo();
            beta = Math.min(beta, bestMove);
            if (beta <= alpha) {
                return bestMove;
            }
        }
        return bestMove;
    }
};

第五步：升級計算權重方法

最初計算權重的方法相當簡單就是通過計算棋盤上棋子所對應的權重，單憑這一點無法判斷棋的局勢。為了改善這一點，我們需要將棋子在棋盤中的位置因素計算在內。比如，騎士在棋盤中間就比在棋盤邊緣位置更優，這樣它可以有更多的選擇。

這里我們在 chess-programming-wiki 所提供的表格的基礎上稍作修改已適應我們的程序。

棋子位置所對應的權重表

這樣我們的 AI 就已經像模像樣了，至少從業余玩家的角度來說。

優化后，[點擊試玩](https://jsfiddle.net/lhartikk/m5q6fgtb/1/)

結語

總的來說，我們所創造的這個簡單的 AI 不會犯一些愚蠢的錯誤，但依舊缺乏大局觀。

通過以上我介紹的方法，已經能夠使我們的 AI 進行基本的對戰。最終 AI 部分的代碼（不包括移動棋子）不足 200 行，這意味著它實現來非常簡單。你可以在 Github 上查看最終版本。

我們還可以繼續優化我們的 AI，比如：

• 落子排序，在 alpha-beta 剪枝的過程中，將可能的最優解先進行探測，從而減少計算量
• 加快遍歷所有落子可能的計算
• 勝負判定

如果你對此感興趣，你可以到 chess programming wiki 中發現更多內容。

感謝閱讀。

更多文章歡迎訪問譯者博客，已升級為 PWA，支持離線訪問、訂閱和添加至桌面。